Example Calculation of Power Strap Width with 5LM, Same Resistivities and Widths, 1W Core Power

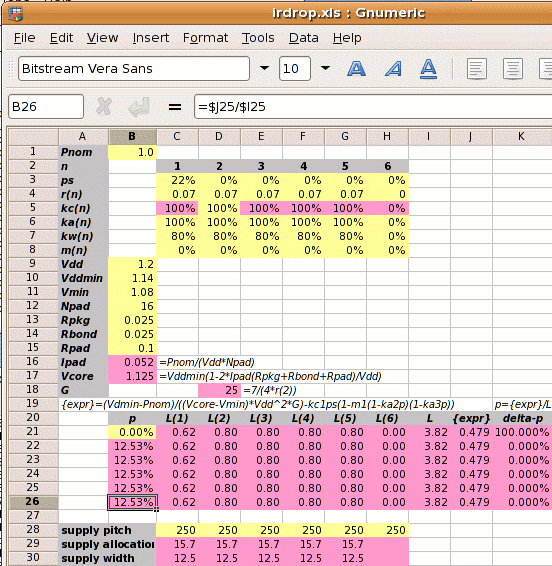
The power strap calculation follows 5 steps.

Step 1: Calculate Ipad and Vcore:

Ipad =	Pnom Vdd × Npad
=	1⁄(1.2×16) = 0.052A

Vcore =	Vddmin(1−2× Ipad ×(Rpkg+Rbond+Rpad))   Vdd
=	1.14×(1−2×0.052×(0.025+0.025+0.1)⁄1.2
=	1.125V

Step 2: Calculate the reference power supply conductance G:

G =	7 4×r2
=	7 ⁄ (4 × 0.07) =	25 mhos

Step 3 is to set out the values of k_an, k_wn, k_cn and m_n for each metal layer, and use these to calculate the value of L.

metal layer 1 2 3 4 5  kan 100% 100% 100% 100% 100% power metal allocated coefficient  kwn  80%  80%  80%  80%  80% power metal used coefficient  kcn 100% 100% 100% 100% 100% conductivity coefficient  mn   0%   0%   0%   0%   0% core area blocked

kan and kcn are 100% because all power straps have the same space allocated and the metal resistivities are the same. kwn is 80% for all metal layers because the power strap widths and spacings are also all the same.

Normally we can't calculate L directly because its value depends on p which we don't know. But in this case with m_1‑5=0 we can

L =	kw1kc1(1-ps)(1-m1(1-ka2p)(1-ka3p))+
	kw2kc2(1-m2(1-ka2p)(1-ka3p))+
	kw3kc3(1-m3(1-ka2p)(1-ka3p))+
	kw4kc4(1-m4(1-ka2p)(1-ka3p))+
	kw5kc5(1-m5(1-ka2p)(1-ka3p))
=	( 0.62 + 0.8 + 0.8 + 0.8 + 0.8 )
=	3.82

Step 4: Calculate the power strap allocation percentage p:

p =	{ Vddmin×Pnom −kc1×ps } ×  1  (Vcore−Vmin)×Vdd2×G L
=	{ 1.14×1 −1×0.22 } × 1 (1.125−1.08)×1.22×25 3.82
=	(0.701−0.222)×0.262 = 12.53%

As shown on the right, a spreadsheet can be used to iterate to the answer. Yellow squares are user input; pink squares are calculated values.

Since in this example all the k_an and k_wn are equal, the strap allocation and widths are the same for each layer.
If we decide to set the power strap pitch to 250µm, then each Vdd and Vss supply strap width W_sn is:

Wsn =

250 × p × kw ⁄ 2 =250 × 0.1253 ×0.8 ⁄ 2 = 12.5µm

Step 5: Calculate the new core size. If the initial core size estimate without power straps is x, then with power straps the core size becomes x′

x′ =	x	=	x	=	x	= x+14.33%
	√(((1-ka2p)(1-ka3p))		√0.87472		0.8747

The value 14.33% is called the IR Drop Adder.

1W is not a very high power consumption, yet 12.5% of each metal layer must be allocated to extra power straps for the required power, and the die side increased by 14.3%.

This is a rather simplified example because the power strap widths and resistivities are the same for all the metal layers. Let's look at a more complex one.