Example Calculation of Power Strap Width with 5LM, 30% Fixed Blocks, Same Resistivities and Widths, 1W Core Power

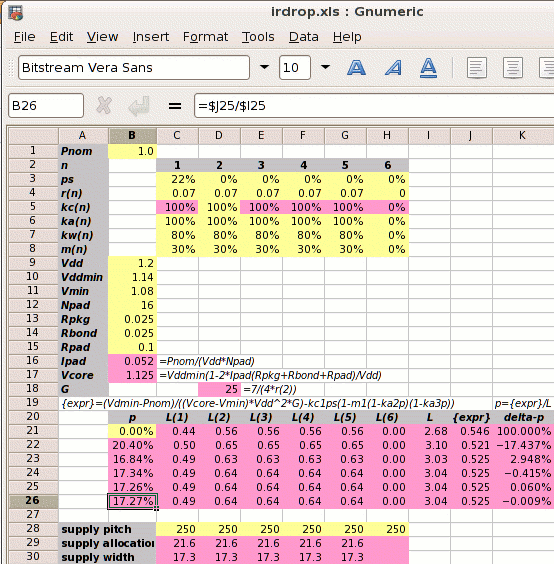
This example is the previous one with 30% of the core area blocked to all metal routing because of fixed blocks. This 30% is the core area before adding power straps.

Step 1: Calculate Ipad and Vcore:

Ipad =	Pnom Vdd × Npad
=	1⁄(1.2×16) = 0.052A

Vcore =	Vddmin(1−2× Ipad ×(Rpkg+Rbond+Rpad))   Vdd
=	1.14×(1−2×0.052×(0.025+0.025+0.1)⁄1.2
=	1.125V

Step 2: Calculate the reference power supply conductance G:

G =	7 4×r2
=	7 ⁄ (4 × 0.07) =	25 mhos

Step 3 is to set out the values of k_an, k_wn, k_cn and m_n for each metal layer, and use these to calculate the value of L.

metal layer 1 2 3 4 5  kan 100% 100% 100% 100% 100% power metal allocated coefficient  kwn  80%  80%  80%  80%  80% power metal used coefficient  kcn 100% 100% 100% 100% 100% conductivity coefficient  mn  30%  30%  30%  30%  30% core area blocked

kan and kcn are 100% because all power straps have the same space allocated and the metal resistivities are the same. kwn is 80% for all metal layers because the power strap widths and spacings are also all the same.

The value of L depends on p which we don't know. We iterate to the solution and use p=0 for the first estimate.

L =	kw1kc1(1-ps)(1-m1(1-ka2p)(1-ka3p))+
	kw2kc2(1-m2(1-ka2p)(1-ka3p))+
	kw3kc3(1-m3(1-ka2p)(1-ka3p))+
	kw4kc4(1-m4(1-ka2p)(1-ka3p))+
	kw5kc5(1-m5(1-ka2p)(1-ka3p))
=	( 0.44 + 0.56 + 0.56 + 0.56 + 0.56 )
=	2.68

Step 4: Calculate the power strap allocation percentage p. The solution must be iterated, and the calculation below shows the first iteration.

m1′ =

m1×(1-ka2p)(1-ka3p)

p =	{ Vddmin×Pnom −kc1×ps(1-m1′) } ×  1  (Vcore−Vmin)×Vdd2×G L
=	{ 1.14×1 −1×0.22×(1-0.3) } × 1 (1.125−1.08)×1.22×25 2.68
=	(0.701−0.156)×0.374 = 20.40%

As shown on the right, a spreadsheet can be used to iterate to the answer of p=17.27%.

The presence of the fixed blocks has increased the percentage of metal which must be allocated to power straps from 12.53% to 17.27%, an increase of 38%.

Step 5: Calculate the new core size. If the initial core size estimate without power straps is x, then with power straps the core size becomes x′

x′ =	x	=	x	=	x	= x+20.88%
	√(((1-ka2p)(1-ka3p))		√0.82732		0.8273

The value 20.88% is called the IR Drop Adder.

Let us look at a more complex example.