Example Calculation of Power Strap Width with 6LM, Different Resistivities and Widths, 2W Core Power

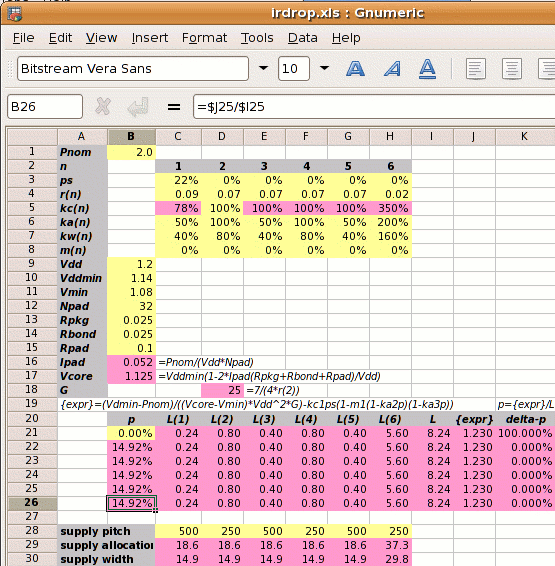
Horizontal power straps are half the width (or twice the pitch) of vertical ones; metal resistivities are different; core power consumption is 2W with 32 core Vdd and 32 core Vss pads.

Step 1: Calculate Ipad and Vcore:

Ipad =	Pnom Vdd × Npad
=	2⁄(1.2×32) = 0.052A

Vcore =	Vddmin(1−2× Ipad ×(Rpkg+Rbond+Rpad))   Vdd
=	1.14×(1−2×0.052×(0.025+0.025+0.1)⁄1.2
=	1.125V

Step 2: Calculate the reference power supply conductance G:

G =	7 4×r2
=	7 ⁄ (4 × 0.07) =	25 mhos

Step 3 is to set out the values of k_an, k_wn, k_cn and m_n for each metal layer, and use these to calculate the value of L.

metal layer 1 2 3 4 5 6  kan  50% 100%  50% 100%  50% 200% power metal allocated coefficient  kwn  80%  80%  80%  80%  80%  80% power metal used coefficient  kcn  78%¹ 100% 100% 100% 100% 350%² conductivity coefficient  mn   0%   0%   0%   0%   0%   0% core area blocked

¹78%=.07/.09; ²350%=.07/.02

Normally we can't calculate L directly because its value depends on p which we don't know. But in this case with m_1‑6=0 we can

L =	kw1kc1(1-ps)(1-m1(1-ka2p)(1-ka3p))+
	kw2kc2(1-m2(1-ka2p)(1-ka3p))+
	kw3kc3(1-m3(1-ka2p)(1-ka3p))+
	kw4kc4(1-m4(1-ka2p)(1-ka3p))+
	kw5kc5(1-m5(1-ka2p)(1-ka3p))+
	kw6kc6(1-m6(1-ka2p)(1-ka3p))
=	( 0.24 + 0.8 + 0.4 + 0.8 + 0.4 + 5.6 )
=	8.24

Step 4: Calculate the power strap allocation percentage p:

p =	{ Vddmin×Pnom −kc1×ps } ×  1  (Vcore−Vmin)×Vdd2×G L
=	{ 1.14×2 −0.78×0.22 } × 1 (1.125−1.08)×1.22×25 8.24
=	(1.403−0.173)×0.121 = 14.92%

As shown on the right, a spreadsheet can be used to iterate to the answer.

If the designer sets the power strap pitch, then the supply allocation for each metal layer n is pitch×k_an×p⁄2 and the supply width is pitch×k_wn×p⁄2. An example is shown in the spreadsheet on the right where we have chosen a vertical power strap pitch of 250µm.

Step 5: Calculate the new core size. If the initial core size estimate without power straps is x, then with power straps the core size becomes x′

x′ =	x	=	x	=	x	= x+12.70%
	√(((1−ka2p)(1−ka3p))		√(0.8508×0.9254)		0.8873

The value 12.7% is called the IR Drop Adder.

This represents a more "normal" power busing scenario (but not necessarily a better one), where vertical power straps are preferred over horizontal ones. The extra use of metal-6 for power straps makes sense (a) because it is a long way from the transistors and so the impact on routing density should be less; and (b) because it is a thick metal layer with better conductivity.

Note the value of L=8.24 of which 5.6 comes from metal-6.